1. Plane-geometry:
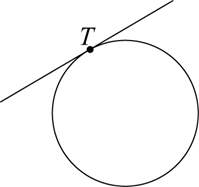
In plane-geometry, a tangent to a circle is a line that intersects a circle at just one point. It touches the circle at that point of contact, but does not pass inside it.
2. Trigonometry:
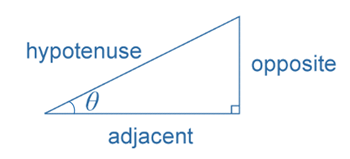
In any right-angled triangle, the tangent of an angle is defined as the length of the side opposite the angle divided by the length of its adjacent side; $$\tan\theta=\frac{\text{opposite}}{\text{adjacent}}$$ , where 0°<θ<90°.
A theorem is a mathematical statement that has been established by means of a proof.
An object is three-dimensional when it possesses the dimensions of height, width and depth. Two dimensional objects only have two dimensions: length and width. A solid is any geometrical object with three-dimensions.
The transformations included in this glossary are enlargements, reflections, rotations, and translations.
Shifting a figure in the plane without turning it is called translation. To describe a translation in the plane, it is enough to say how far left or right and how far up or down the figure is moved.
A translation is a transformation that moves each point to its translation image.
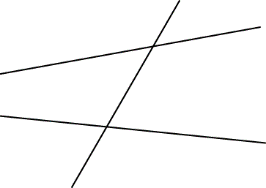
A transversal is a line that crosses two or more other lines in a plane.
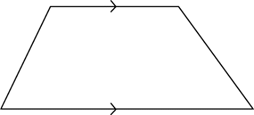
A trapezium is a quadrilateral with one pair of opposite sides parallel.
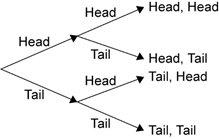
A tree diagram is a diagram that can used to enumerate the outcomes of a multi-step random experiment.
The diagram below shows a tree diagram that has been used to enumerate all of the possible outcomes when a coin is tossed twice. Below is an example of a two-step random experiment.
A triangular number is the number of dots required to make a triangular array of dots in which the top row consists of just one dot, and each of the other rows contains one more dot than the row above it. So the first triangular number is 1, the second is 3=1+2, the third is 6 (=1+2+3) and so on.

Trigonometric ratios describe the relationships between the angles and sides of right triangles. The three basic trigonometric ratios covered in this glossary are: Sine, Cosine, and Tangent.
A shape is two-dimensional when it only possesses the dimensions of length and width.
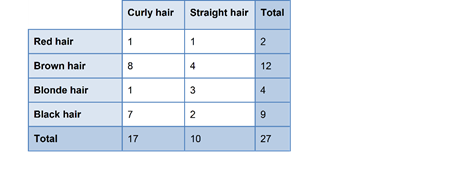
A two-way table is commonly used to for displaying the two-way frequency distribution that arises when a group of individuals or things are categorised according to two criteria; for example, the two-way table below displays the two-way frequency distribution that arises when 27 children are categorised according to hair type (straight or curly) and hair colour (red, brown, blonde, black).
The information in a two-way table can also be displayed graphically using a side-by-side column graph.