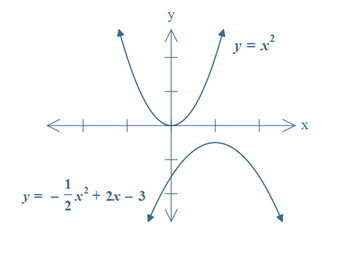
In algebra, a parabola is the graph of a function of the general form $$y=ax^2+bx+c$$, where a, b and c are real numbers and a≠0. Two examples of parabolas are shown below.
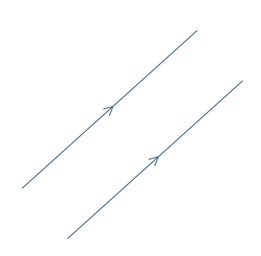
Parallel lines are lines in a plane which do not intersect or touch each other at any point. Parallel lines can never intersect, even if they were to continuously extend toward infinity.
Two lines are parallel, if they have the same gradient (or slope).
The lines below are parallel to one another, as indicated by the use of the arrow signs. In text, the symbol ∥ is used to denote parallel lines; for example, a∥b is read as “line a is parallel to line b”.
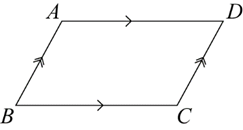
A parallelogram is a quadrilateral whose opposite sides are parallel.
Thus the quadrilateral ABCD shown below is a parallelogram because AB∥DC and AD∥BC.
Properties of a parallelogram
- The opposite angles of a parallelogram are equal.
- The opposite sides of a parallelogram are equal.
- The diagonals of a parallelogram bisect each other.
Partitioning means dividing a quantity into parts. In the early years, it commonly refers to the ability to think about numbers as made up of two parts, such as, 10 is 8 and 2. In later years it refers to dividing both continuous and discrete quantities into equal parts.
A percentage is a fraction whose denominator is 100; for example, 6 percent (written as 6%) is the percentage whose value is $$\frac6{100}$$.
Similarly, 40 as a percentage of 250 is $$\frac{40}{250}\times100=16\%$$.
Percentiles are the 99 values that divide an ordered data set into 100 (approximately) equal parts. It is only possible to divide a data set into exactly 100 equal parts when the number of data values is a multiple of one hundred.
Within the above limitations, the first percentile divides off the lower 1% of data values. The second, the lower 2% and so on. In particular, the lower quartile (Q1) is the 25th percentile, the median is the 50th percentile and the upper quartile is the 75th percentile.
Percentiles are often used to report comparative test results. A student who scores in the 90th percentile for a given test has scored higher than 90% of other students who took the test. A student who scores in the 10th percentile would have scored better than only 10% of students who took the test.
The perimeter of a plane figure is the length of its boundary. The perimeter of a figure can be calculated by adding the lengths of all its sides.
In geometry, two lines are said to be perpendicular to each other, if they meet at a right angle (90 degrees).
Pi is the name of the Greek letter π that is used to denote the ratio of the circumference of any circle to its diameter. The number $$\pi$$ is irrational, but $$\frac{22}7$$ is a rational approximation. The decimal expansion of $$\pi$$ begins:
$$\pi=3.141\text{ }592\text{ }653\text{ }589\text{ }79\dots$$
A picture graph is a statistical graph for organising and displaying categorical data.

Place value refers to the value of a digit as determined by its position in a number, relative to the ones (or units) place. For integers, the ones place is occupied by the rightmost digit in the number; for example, in the number 2 594.6 the 4 denotes 4 ones, the 9 denotes 90 ones or 9 tens, the 5 denotes 500 ones or 5 hundreds, the 2 denotes 2000 ones or 2 thousands, and the 6 denotes $$\frac6{10}$$ of a one or 6 tenths.
A point marks a position, but has no size.
A polygon is a plane figure bounded by three or more line segments. The word derives from Greek polys “many” and gonia “angle”.
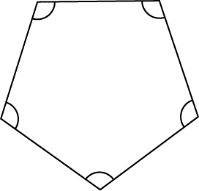
The regular pentagon shown below is an example of a polygon. It is called a pentagon because it has five sides (and five angles). It is called regular because all sides have equal length and all interior angles are equal.
A polyhedron is a three-dimensional object, or a solid, which consists of a collection of polygons, joined at their edges and making up the faces of the solid. The word derives from Greek polys “many” and hedra “base” or “seat”.
The solid below is an example of a polyhedron (called an icosahedra and consisting of 20 faces).

A polynomial in one variable $$x$$ is a finite sum of terms of the form $$ax^k$$, where $$a$$ is a real number and $$k$$ is a non-negative integer.
A non-zero polynomial can be written in the form $$a_0+a_1x+a_2x^2+\cdots+a_nx^n,$$, where $$n$$ is a non-negative integer and $$a_n\neq0$$.
The term that contains the variable $$x$$ raised to the highest power, that is $$a_nx^n$$, is called the leading term.
The numbers $$a_0,a_1,\dots,a_n$$ are called the coefficients of the terms. Coefficients include the preceding sign.
For example, in the polynomial $$3x^2-5x+2$$, the leading term is $$3x^2$$ and the coefficient of the second term is $$-5$$.
A population is the complete set of individuals, objects, places etc. about which we want information.
A census is an attempt to collect information about the whole population.
A positive integer is an integer that excludes negative numbers and zero. Positive integers are 1, 2, 3, 4, 5, 6, ….
Primary data is original data collected by the user. Primary data might include data obtained from interviews the user has conducted herself, or observations the user has made during an experiment.
A prime factor of a number is a factor of that number which is prime.
A prime number is a natural number greater than 1 that has no factor other than 1 and itself.
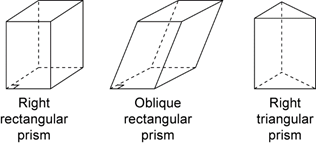
A prism is a polyhedron that has two congruent and parallel faces and all its remaining faces are parallelograms.
A right prism is a polyhedron that has two congruent and parallel faces and all its remaining faces are rectangles. A prism that is not a right prism is often called an oblique prism.
Some examples of prisms are shown below.
The probability of an event is a number between 0 and 1 that indicates the chance of that event happening; for example, the probability that the sun will come up tomorrow is 1, the probability that a fair coin will come up ‘heads’ when tossed is 0.5, while the probability of someone being physically present in Adelaide and Brisbane at exactly the same time is zero.
A product is the result of multiplying together two or more numbers or algebraic expressions; for example, 36 is the product of 9 and 4, and $$x^2-y^2$$ is product of $$x-y$$ and $$x+y$$.
A proof is a rigorous mathematical argument that demonstrates the truth of a given proposition. A mathematical statement that has been established by means of a proof is called a theorem.
Two quantities are in proportion, if there is a constant ratio between them.
A protractor is an instrument for measuring angles. It uses degrees as the unit of measurement and is commonly in the shape of a semi-circle (180°) or circle (360°).
A pyramid is a polyhedron with a polygonal base and triangular sides that meet at a point called the vertex. The pyramid is named according to the shape of its base.
Pythagoras’ theorem states that for a right-angled triangle:
The square of the hypotenuse of a right-angled triangle equals the sum of the squares of the lengths of the other two sides.
In symbols, $$c^2=a^2+b^2$$.
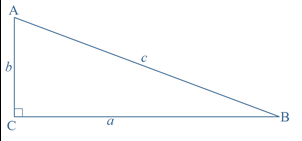
The converse
If $$c^2=a^2+b^2$$ in a triangle ABC, then ∠C is a right angle.