In the given context, capacity is a term that describes how much a container will hold. It is used in reference to the volume of fluids or gases and is measured in units such as litres or millilitres.
The Cartesian plane or Cartesian coordinate system is a system that describes the exact location of any point in a plane using an ordered pair of numbers, called coordinates. It is defined by the intersection of a horizontal and vertical number line at a point called the origin. The coordinates of the origin are (0, 0).
The Cartesian plane is divided into four quadrants by these perpendicular axes called the x-axis (horizontal line) and the y-axis (vertical line). The axes can be used to identify any point in the plane using a pair of coordinates, as shown in the diagram below.
A categorical variable is a variable whose values are categories. For example, blood group is a categorical variable; its common values are: A, B, AB or O.
A census is a survey of a whole population.
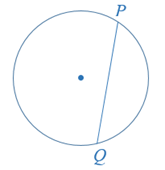
A chord in a circle is a line segment joining any two points on the circle. Chord PQ, illustrated below, joins points P and Q.
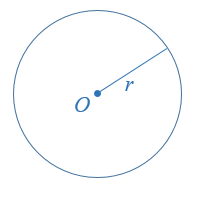
A circle, with centre O and radius r, is the set of all points on a plane whose distance from O is r.
Circumference refers to the boundary of a circle. The length of the circumference c is given by \(c=\pi d\), where d is the diameter. Alternatively, it is given by \(c=2\pi r\), where r is the radius.
Angles are classified according to their size. See acute angle, obtuse angle, reflex angle, right angle, straight angle and revolution.
Co-interior angles lie between two lines and on the same side of a transversal.
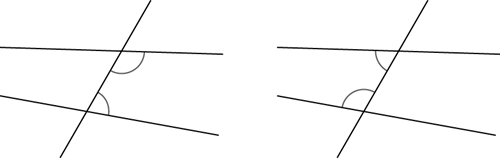
In each diagram the two marked angles are called co-interior angles.
If the two lines are parallel, then co-interior angles add to give 180o and so are supplementary. In the diagram below the angles ∠CGF and ∠AFG are supplementary.
Conversely, if a pair of angles are supplementary, then the lines are parallel. Line segment CD is parallel to line segment AB, because ∠CGF + ∠AFG = 180°.
A column graph is a graph used in statistics for organising and displaying categorical data. It consists of a series of equal-width rectangular columns, one for each category. Each column has a height equal to the frequency of the category. This is shown in the example below which displays the hair colours of 27 students.
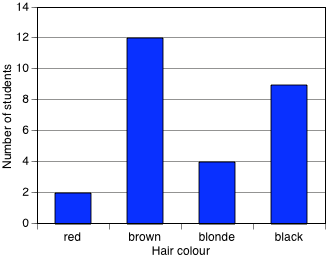
Column graphs are frequently called bar graphs or bar charts. In a bar graph or chart, the bars can be either vertical or horizontal.
A common factor (or common divisor) of a set of numbers or algebraic expressions is a factor of each element of that set. For example, 6 is a common factor of 24, 54 and 66, since \(24=6\times4\), \(54=6\times9\), and \(66=6\times11\). Similarly, \(x+1\) is a common factor of \(x^2-1\) and \(x^2+5x+4\), since \(x^2-1\;=(x+1)(x-1)\) and \(x^2+5x+4\;=(x+1)(x+4)\).
Operations are commutative if the order in which terms are given does not affect the result.
The commutative law for addition is: \(a+b=b+a\) for all numbers a and b.
For example, 3+5=5+3.
The commutative law for multiplication is: \(ab=ba\) for all numbers a and b.
For example, 4×7=7×4.
Subtraction and division are not commutative because 5-3≠3-5 and 12÷4≠4÷12.
Two angles that add to 90o are called complementary; for example, 23o and 67o are complementary angles.
Events A and B are complementary events if A and B are mutually exclusive (have no overlap) and \(\;Pr(A)\;+\;Pr(B)\;=\;1\), where the symbol \(Pr(A)\;\) denotes the probability of event \(A\) occurring.
A composite number is a natural number that has a factor other than 1 and itself.
The interest earned by investing a sum of money (the principal) is compound interest if each successive interest payment is added to the principal for the purpose of calculating the next interest payment. For example, if the principal \(\$P\) earns compound interest at the rate of r% per period, then after n periods the principal plus interest is \(\;\$P(1+r)^n\).
Computation is mathematical calculation.
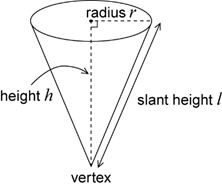
A cone is a solid that is formed by taking a circle, called the base, and a point, called the vertex, which lies above or below the circle, and joining the vertex to each point on the circle.
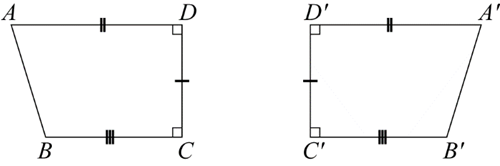
Two plane shapes are congruent if they are identical in size and shape and one can be moved or reflected so that it fits exactly on top of the other figure.
Matching sides have the same length, and matching angles have the same size.
The four standard congruence tests for triangles
Two triangles are congruent if:
SSS: the three sides of one triangle are respectively equal to the three sides of the other triangle, or
SAS: two sides and the included angle of one triangle are respectively equal to two sides and the included angle of the other triangle, or
AAS: two angles and one side of one triangle are respectively equal to two angles and the matching side of the other triangle, or
RHS: the hypotenuse and one side of one right‐angled triangle are respectively equal to the hypotenuse and one side of the other right‐angled triangle.
Continuous numerical data includes any value that lies within an interval. In practice, the values taken are subject to the accuracy of the measurement instrument used to obtain these values. Height, reaction time to a stimulus and systolic blood pressure are all types of continuous numerical data that can be collected.
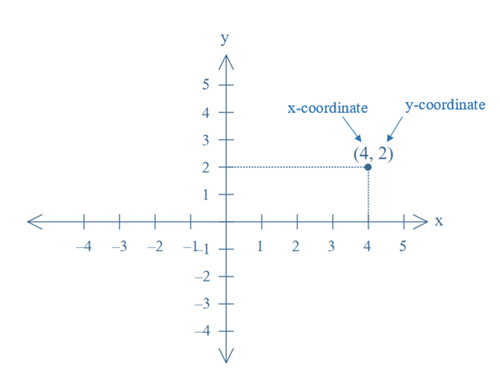
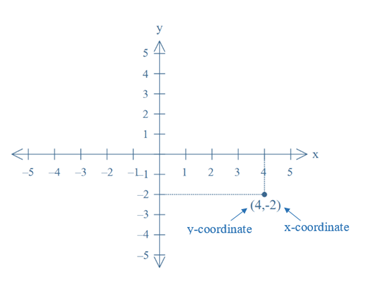
A coordinate is one value of an ordered pair that describes the location of a point along an axis in the Cartesian plane. By definition, the first number (xcoordinate) of the ordered pair denotes the horizontal distance, the second number (ycoordinate) gives the vertical distance from the centre (origin) of the coordinate system. Positive x coordinates indicate that the point is located to the right (East), negative to the left (West) of the origin. Positive y coordinates indicate a location above (North of), negative below (South of) the origin. The origin has the coordinates (0,0).
For instance, in the ordered pair (4, –2) the number 4 denotes the x coordinate of a point situated at a horizontal distance of 4 units to the origin. The number –2 denotes the y coordinate of the same point indicating a vertical distance of 2 units below the origin.
see Cartesian plane.
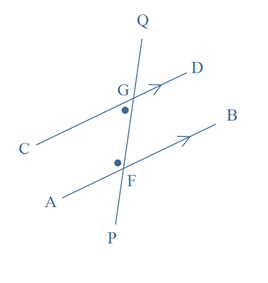
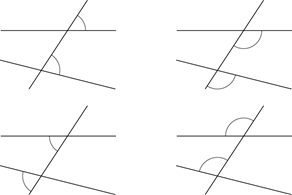
Corresponding angles are formed when two lines are crossed by another line (the transversal). In each diagram the two marked angles are called corresponding angles because they are on the same side of the transversal and in corresponding positions in relation to the lines.
If the lines are parallel, then each pair of corresponding angles is equal (as are the angles ∠QGD and ∠GFB in the diagram shown below).
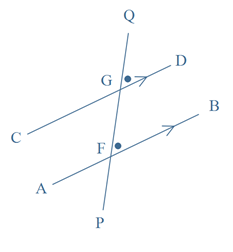
Conversely, if a pair of corresponding angles is equal, then the lines are parallel.
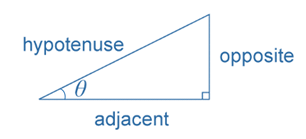
In any right-angled triangle, \(\cos\theta=\frac{\text{adjacent}}{\text{hypotenuse}}\), where \(0<\theta<90^\circ\).
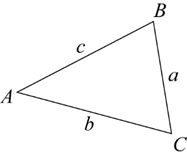
In any triangle ABC, \(c^2=a^2+b^2-2ab\cos C\)
Counting numbers are the positive integers, that is, the numbers 1, 2, 3, … .
Sometimes it is taken to mean the non-negative integers, which include zero.
Counting on is a strategy for solving simple addition problems. For example, a student can add 6 and 4 by counting on from 6, saying ‘7, 8, 9, 10’. If students are asked how many more objects need to be added to a collection of 8 to give a total of 13, they can count ‘9, 10, 11, 12, 13’ to find the answer 5.
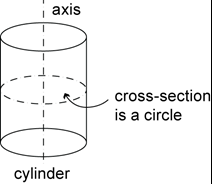
A cylinder is a solid that has parallel circular discs of equal radius at the ends, and whose horizontal cross-section is a circle with the same radius. The centres of these circular cross-sections lie on a straight line, called the axis of the cylinder.