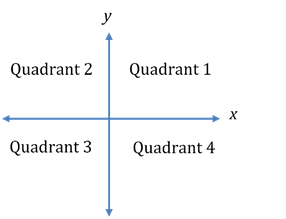
Quadrant refers to the four sections of the Cartesian plane created through the intersection of the x and y-axes. They are numbered 1 through 4, beginning with the top right quadrant and moving counter clockwise around the plane. Each of the four quadrants is labelled on the plane below.
The general quadratic equation in one variable is $$ax^2+bx+c=0,$$ where $$a≠0$$.
The solutions are given by the quadratic formula: $$x=\frac{-b\pm\sqrt[{}]{b^2-4ac}}{2a}$$.
A quadratic expression or function contains one or more terms in which the variable is raised to the second power, but no variable is raised to a higher power. Examples of quadratic expressions include $$3x^2+7$$ and $$x^2+2xy+y^2-2x+y+5$$.
A quadrilateral is a polygon with four sides.
Quartiles are the values that divide an ordered data set into four (approximately) equal parts. It is only possible to divide a data set into exactly four equal parts, when the number of data values is a multiple of four.
There are three quartiles. The first, the lower quartile (Q1) divides off (approximately) the lower 25% of data values. The second quartile (Q2) is the median. The third quartile, the upper quartile (Q3), divides off (approximately) the upper 25% of data values.
A quotient is the result of dividing one number or algebraic expression by another. See also remainder.