The gradient of a line is sometimes also called a slope and is a measure of how steeply a line is rising or falling.
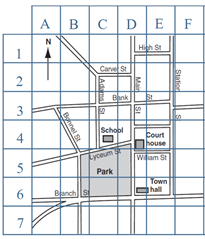
If \(A(x_1,y_1)\) and \(B(x_2,y_2)\) are points on the plane, the gradient of the line segment AB is given by
\(AB=\frac{\text{rise}}{\text{run}}=\frac{y_2-y_1}{x_2-x_1}\), provided that \(x_2-x_1\neq0\)
The gradient of a line is the gradient of any line segment within the line.
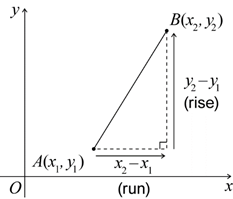
Gradients can be positive or negative, indicating whether the line is increasing or decreasing from left to right. The graph below shows two examples:
\(gradient(AB)=\frac{3-1}{-1-(-4)}=\frac23\)
\(gradient(CD)=\frac{0-4}{3-1}=\frac{-4}2=-2\)
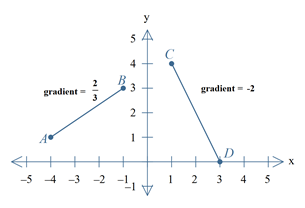
A grid reference identifies a region on a map. Coordinates and gridlines are used to refer to specific features or locations. For example, in the map below, the school is located at the grid reference C4.