An acute angle is bigger than
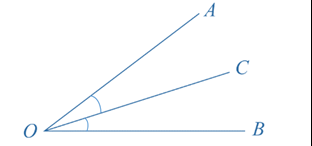
Adjacent angles share a common ray and a common vertex, and lie on opposite sides of the common ray. In the diagram, ∠AOC and ∠COB are adjacent angles.
An algebraic expression is formed by combining numbers and algebraic terms using arithmetic operations (addition, subtraction, multiplication, division, and exponentiation). The expression must be unambiguous. For example, \(a^2+3ab-2b^2\) is an algebraic expression, but \(2x+\div3\) is not one because it is ambiguous.
An algebraic fraction is a fraction in which both, numerator and denominator, are algebraic expressions.
An algebraic term forms a part of an algebraic expression. For example, \(\;2,\text{ }3x\), and \(\;5x^2\) are terms of the algebraic expression \(2+3x-5x^2.\). Terms are separated by + or – signs.
Alternate angles are formed when two lines are crossed by another line (the transversal). The alternate angles are on opposite sides of the transversal, but inside the two lines. In each diagram below, the two marked angles are alternate angles as they are on opposite sides of the transversal.
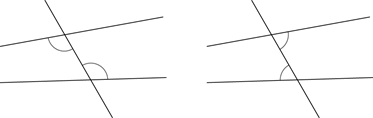
If the lines AB and CD are parallel, then each pair of alternate angles are equal.
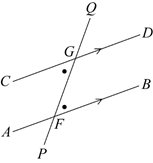
Conversely, if a pair of alternate angles are equal, then the lines are parallel. Line segment CD is parallel to line segment AB, because ∠CGF equals ∠GFB.
An angle is the figure formed by the rotation of a ray about a point, called the vertex of the angle. The size of an angle is usually measured in degrees (°).
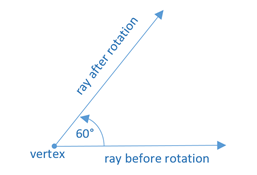
There are different ways of depicting and naming angles. Angles may be depicted using as symbol such as an arc, a dot or a letter (often from the Greek alphabet). Angles are named using different conventions, such as the angle symbol ∠ followed by three letters denoting points, where the middle letter is the vertex, or using just the label of the vertex.
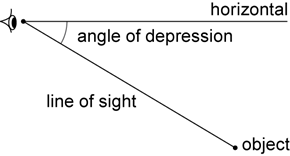
When an observer looks at an object that is lower than the eye of the observer, the angle between the line of sight and the horizontal is called the angle of depression.
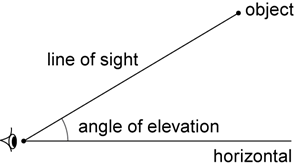
When an observer looks at an object that is higher than the eye of the observer, the angle between the line of sight and the horizontal is called the angle of elevation.
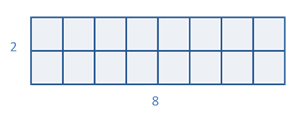
Area is a measure of how many units are required to cover a surface. The units are usually standard units, such as square centimetres or square metres. The area of a rectangle can be found by multiplying the size of its length by the size of its width. For example, the area of the rectangle below is given by 8×2=16 units.
An array is an ordered collection of objects or numbers. Rectangular arrays are commonly used in primary mathematics. For example, the two arrays of dots shown below are two different representations of the number 24.

Operations are associative if the order in which operations take place does not affect the result.
For example, addition of numbers is associative, since the order in which they are added does not change their sum. The corresponding associative law is: (a+b)+c=a+(b+c) for all numbers a,b and c.
Multiplication is also associative, as the product of the numbers does not vary with the order of their multiplication. The corresponding associative law is: (ab)c=a(bc) for all numbers a,b and c.
Subtraction and division are not associative, as the order of operations changes the value of the expression; for example: (7-4)-3≠7-(4-3) and (12÷6)÷2≠12÷(6÷2).
An average is a number expressing a central or typical value in a set of data. While it usually refers to the arithmetic mean, that is, the sum of a set of numbers divided by the number of numbers in the set, it may also refer to other measures of central tendency.
(plural) See axis.
(singular) An axis is one of the horizontal or vertical lines that make up the Cartesian plane. The horizontal line is called the \(x\) axis, and the vertical line is called the \(y\) axis. The \(x\) and \(y\) axes intersect at point O, called the origin, which defines the centre of the coordinate system.