Understanding
Portfolio summary
In F–2, students make connections between related concepts and progressively apply the familiar to develop new ideas.
In Years 3–6, students make connections between related concepts and progressively apply the familiar to develop new ideas. They develop an understanding of the relationship between the ‘why’ and the ‘how’ of mathematics. Students build understanding when they connect related ideas.
In Years 7–8, students build a robust knowledge of adaptable and transferable mathematical concepts. They make connections between related concepts and progressively apply the familiar to develop new ideas. They develop an understanding of the relationship between the ‘why’ and the ‘how’ of mathematics. Students build understanding when they connect related ideas, when they represent concepts in different ways, and when they describe their thinking mathematically.
In Years 9–10, students build a robust knowledge of adaptable and transferable mathematical concepts. They make connections between related concepts and progressively apply the familiar to develop new ideas. They develop an understanding of the relationship between the ‘why’ and the ‘how’ of mathematics. Students build understanding when they connect related ideas, when they represent concepts in different ways, when they identify commonalities and differences between aspects of content, when they describe their thinking mathematically, and when they interpret mathematical information.
Work samples
View the proficiencies across F–10
Year 3 includes connecting number representations with number sequences, partitioning and combining numbers flexibly, representing unit fractions, using appropriate language to communicate times, and identifying environmental symmetry.
Year 4 includes making connections between representations of numbers, partitioning and combining numbers flexibly, extending place value to decimals, using appropriate language to communicate times and describing properties of symmetrical shapes.
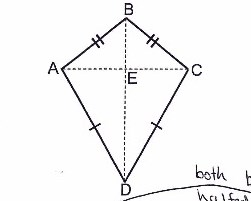
Year 5 includes making connections between representations of numbers, using fractions to represent probabilities, comparing and ordering fractions and decimals and representing them in various ways, describing transformations and identifying line and rotational symmetry.
Year 6 includes describing properties of different sets of numbers, using fractions and decimals to describe probabilities, representing fractions and decimals in various ways and describing connections between them, and making reasonable estimations.
Year 7 includes describing properties of different sets of numbers, using fractions and decimals to describe probabilities, representing fractions and decimals in various ways and describing connections between them, and making reasonable estimations.
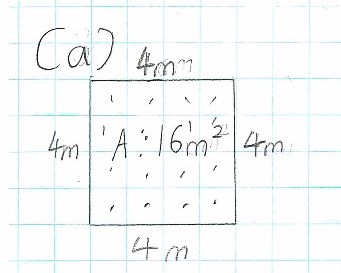
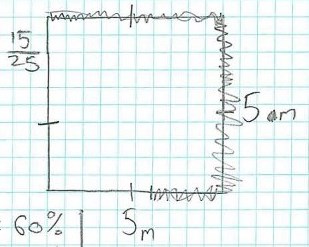
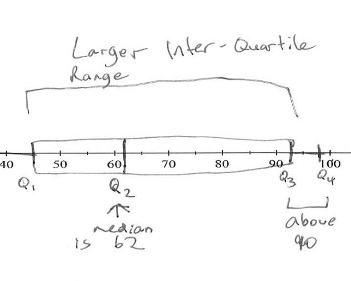
Year 8 includes describing patterns involving indices and recurring decimals, identifying commonalities between operations with algebra and arithmetic, connecting rules for linear relations with their graphs, explaining the purpose of statistical measures and explaining measurements of perimeter and area.
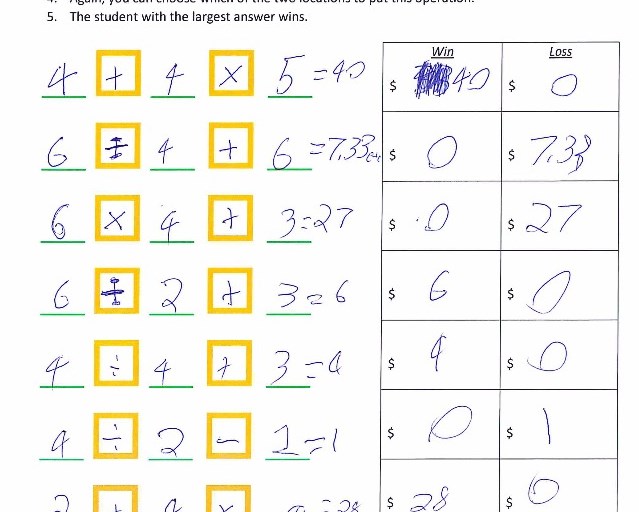
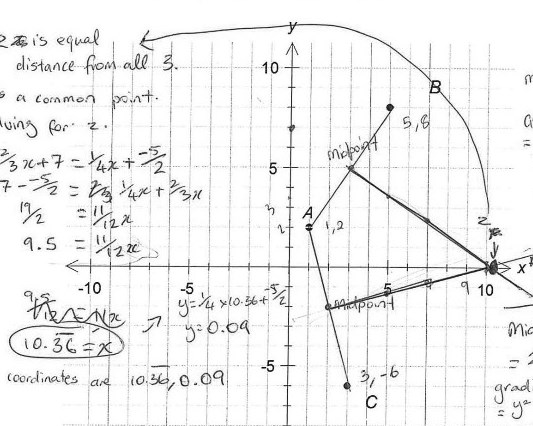
Year 9 includes describing the relationship between graphs and equations, simplifying a range of algebraic expressions and explaining the use of relative frequencies to estimate probabilities and of the trigonometric ratios for right-angle triangles.
Year 10 includes applying the four operations to algebraic fractions, finding unknowns in formulas after substitution, making the connection between equations of relations and their graphs, comparing simple and compound interest in financial contexts and determining probabilities of two- and three-step experiments.